Wprowadzenie

Teoria płyt Reissnera–Mindlina jest rozszerzeniem teorii płyt Kirchhoffa–Love’a, które uwzględnia odkształcenia postaciowe (ścinanie) na grubości płyty. Teoria została zaproponowana w 1951 roku przez Raymonda Mindlina. Podobną, choć nie identyczną teorię w ujęciu statycznym zaproponował wcześniej, w 1945 roku, Eric Reissner. Obie teorie są przeznaczone do opisu grubych płyt, w których normalna do powierzchni środkowej pozostaje prostą, lecz niekoniecznie prostopadłą do tej powierzchni. Teoria Reissnera–Mindlina służy do obliczania odkształceń i naprężeń w płycie, której grubość stanowi około jedną dziesiątą wymiarów płaskich, podczas gdy teoria Kirchhoffa–Love’a ma zastosowanie do cieńszych płyt.

Analogicznie do rozszerzenia klasycznej teorii belki Bernoulliego–Eulera przez Timoszenkę, w ujęciu płytowym przyjmuje się, że włókno materiału prostopadłe do powierzchni środkowej pozostaje linią prostą po odkształceniu, choć jego orientacja względem zdeformowanej powierzchni może ulec zmianie. Pomijając wpływ stanu tarczowego, zakładamy więc, że przemieszczenia płyty można opisać poprzez odpowiednio zdefiniowane pole przemieszczeń, które uwzględnia zarówno ugięcie, jak i obrót przekrojów normalnych wzdłuż grubości elementu.

Założenia i zakres stosowania teorii płyt Mindlina-Reissnera

• Rozpatrywana jest płyta o grubości $h$, której powierzchnia środkowa opisana jest współrzędnymi $x_1, x_2$, natomiast współrzędna $x_3$ mierzona jest w kierunku grubości, w zakresie $-h/2 \leq x_3 \leq h/2$.

• W odróżnieniu od klasycznej teorii Kirchhoffa--Love’a dopuszcza się odkształcenia ścinające w kierunku grubości. Jest to istotne przy analizie płyt o niepomijalnej grubości, gdzie stosunek $h$ do wymiarów w~płaszczyźnie nie jest bardzo mały.

• Kinematyka odkształceń: normalne do powierzchni środkowej pozostają po odkształceniu prostymi, lecz nie muszą pozostawać prostopadłe do powierzchni środkowej. Oznacza to, że obrót normalnych jest swobodny.

• Wersja liniowa teorii zakłada małe odkształcenia oraz małe kąty obrotu. Materiał jest liniowo sprężysty.

• Przyjmuje się, że naprężenia normalne w kierunku grubości są pomijalnie małe, tzn. $\sigma_{33} \approx 0$. W rezultacie uzyskuje się płaski stan naprężenia.

• Teoria Mindlina--Reissnera jest bardziej ogólna od teorii Kirchhoffa- Love’a i pozwala poprawnie opisywać zachowanie tzw. grubszych płyt. W granicy bardzo małej grubości wyniki obu teorii są zbieżne.

Funkcje opisujące przemieszczenia

Funkcje przemieszczeń zakłada się w następującej postaci (pomijamy stan tarczowy)

$$u_1 = \phi_1 \cdot x_3, \quad u_2 = \phi_2 \cdot x_3, \quad u_3 = w.$$

Do opisu deformacji konieczne jest wyznaczenie trzech funkcji zmiennych $w(x_1, x_2)$ - ugięcie płyty, $\phi_1(x_1, x_2)$ - obrót normalnej do powierzchni środkowej płyty wokół osi $x_2$, $\phi_1(x_1, x_2)$ - obrót normalnej do powierzchni środkowej płyty wokół osi $x_1$.

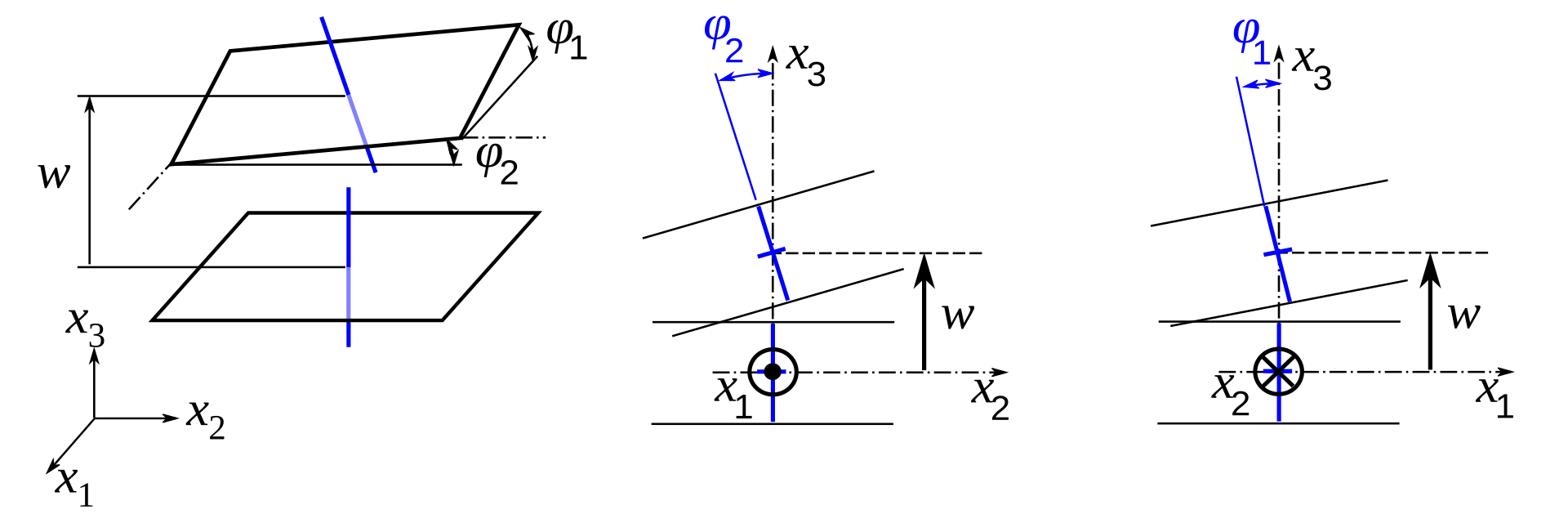
Pole odkształcenia

Wykorzystując związki geometryczne które łączą gradienty pola przemieszczenia z odkształceniem dostajemy następujące relacje

$$\varepsilon_{11} =\pp{\phi_1}{x_1} x_3$$ $$\varepsilon_{22} =\pp{\phi_2}{x_2} x_3$$ $$\varepsilon_{33} = 0$$ $$\varepsilon_{12} = \cfrac12 \left( \pp{\phi_1}{x_2} + \pp{\phi_2}{x_1}\right) x_3$$ $$\varepsilon_{13} = \cfrac12 \left( \phi_1 + \pp{w}{x_1}\right)$$ $$\varepsilon_{23} = \cfrac12 \left( \phi_2 + \pp{w}{x_2}\right)$$

Pole naprężenia

Zakładając że płyta jest izotropowa, składowe tensora naprężenia wyznaczamy stosują liniowe prawe Hooke'a

$$\sigma_{ij} = C_{ijkl}\varepsilon_{kl}$$ $$\sigma_{11} = \cfrac{E}{1-\nu^2}\left( \pp{\phi_1}{x_1} + \nu \pp{\phi_2}{x_2}\right) x_3$$ $$\sigma_{22} = \cfrac{E}{1-\nu^2}\left( \pp{\phi_2}{x_2} + \nu \pp{\phi_1}{x_1}\right) x_3$$ $$\sigma_{12} = \cfrac{E}{2+\nu}\left( \pp{\phi_1}{x_2} + \pp{\phi_2}{x_1}\right) x_3$$ $$\sigma_{23} = G \left( \phi_2 + \pp{w}{x_2} \right)$$ $$\sigma_{13} = G \left( \phi_1 + \pp{w}{x_1} \right)$$

Momenty

Momenty wyznaczamy całkując naprężenia po grubości płyty przemnożone przez współrzędną po grubości płyty. Otrzymujemy wtedy

$$M_{11} = \int_{-h/2}^{h/2} x_3 \sigma_{11} dx_3 = D \left( \pp{\phi_1}{x_1}+\nu \pp{\phi_2}{x_2}\right)$$ $$M_{22} = \int_{-h/2}^{h/2} x_3 \sigma_{22} dx_3 = D \left( \pp{\phi_2}{x_2}+\nu \pp{\phi_1}{x_1}\right)$$ $$M_{12} = \int_{-h/2}^{h/2} x_3 \sigma_{12} dx_3 = \cfrac{1-\nu}{2}D \left( \pp{\phi_1}{x_2}+\pp{\phi_2}{x_1}\right)$$

Stała $D$ jest sztywnością płytową, zdefiniowaną tak samo jak w teorii Kirchhoffa–Love'a.